Trabajo de Geometría

Índice.

1. El triángulo
2. Lugares geométricos
3. Movimientos en el plano
4. Resumen de áreas y volúmenes de figuras conocidas 
5. La esfera y el globo terráqueo
6. Bibliografía

1. El triángulo

 1.1. Propiedades y tipos de triángulos

Las propiedades de los triángulos son las siguientes:

• Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.

• La suma de los ángulos interiores de un triángulo es igual a 180°.

• El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.

Hay dos modos de clasificar los triángulos, según sus lados y según sus ángulos.

Según sus lados:

• Equilátero: todos los lados son iguales
• Isósceles: tiene dos lados iguales.
• Escaleno: no tiene ningún lado igual.

Según sus ángulos:

• Rectángulos: si tienen un ángulo recto (60º).
• Acutángulos: si tienen tres lados agudos (-90º).
• Obtusángulos: si tienen un ángulo obtuso (+90º).

 1.2. Rectas y puntos notables de un triángulo

Con respecto a los distintos tipos de centros del triángulo existen varios tipos:

• Incentro: es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma. en concreto, es el punto de intersección de las bisectrices de cada uno de los ángulos del triángulo. Para representarlo graficamente debemos dibujar las 3 bisectrices y localizar el punto de intersección de las mismas.

• Baricentro: es el punto de intersección de las medianas de dicho triángulo. Para representarlo graficamente debemos dibujar las 3 medianas y localizar el punto en el que se cortan.

• Circuncentro: es el centro de la circunferencia circunscrita al triángulo, por lo que la distancia a cada uno de sus vértices es la misma. En concreto, es el punto de intersección de las mediatrices del triángulo. Para representarlo graficamente dibujamos las 3 mediatrices y localizamos el punto de intersección de las mismas.

• Ortocentro: es el punto de intersección de las 3 alturas del triángulo. Para representarlo graficamente dibujamos las 3 alturas y nos quedamos con el punto en el que se intersecan.

A continuación, tenéis un iframe de GeoGebra donde podéis verlo más claramente.

Podéis seleccionar lo que queráis ver, mover el triángulo, y algunas cosillas más a vuestro gusto.

 1.3. El teorema de Pitágoras

El teorema de Pitágoras dice que, en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

A al cuadrado más B al cuadrado es igual a C al cuadrado

Cada uno de los sumandos, representa el área de un cuadrado de lado a, b, c. Con lo que la expresión anterior, en términos de áreas se expresa en la forma siguiente:

El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

Aquí tenéis, otra vez más, un iframe de GeoGebra, mediante el cual podéis ver más gráficamente el teorema de Pitágoras.

Con este vídeo, podéis ver la demostración del teorema de Pitágoras en 3D: Clic aquí

 1.4. El teorema de Tales

El teorema de Tales dice que si 2 rectas cualesquiera son cortadas por rectas paralelas, los segmentos que determina en una de las rectas son proporcionales a los segmentos correspondiente de la otra.

Este teorema nos permite calcular, por tanto, la longitud de un segmento si conocemos su correspondiente en la otra recta y la proporción entre ambos.

Con la canción de "Les Luthiers - Teorema de Tales", se entiende bastante bien, y el vídeo lo muestra bastante bien, si lo queréis ver/oír, aquí tenéis el enlace: Clic aquí

La letra de la canción es la siguiente:

Si tres o más paralelas

Si tres o más parale-le-le-las

Si tres o más paralelas

Si tres o más parale-le-le-las

son cortadas, son cortadas

por dos transversales, dos transversales,

son cortadas, son cortadas

por dos transversales, dos transversales,

Si tres o más parale-le-le-las

Si tres o más parale-le-le-las

son cortadas, son cortadas,

son cortadas, son cortadas

(Entre voces en son cortadas: "Son transversales")

Dos segmentos de una de estas, dos segmentos cualesquiera,

dos segmentos de una de estas son proporcionales

a los dos segmentos correspondientes de la otra.

Hipótesis:

A paralela a B,

B paralela a C,

A paralela a B, paralela a C, paralela a D.

O-P es a P-Q,

M-N es a N-T,

OP es a PQ como MN es a NT.

A paralela a B,

B paralela a C,

OP es a PQ como MN es a NT.

La bisectriz yo trazaré

y a cuatro planos intersectaré.

Una igualdad yo encontraré:

OP+PQ es igual a ST.

Usaré la hipotenusa.

Ay, no te compliques, nadie la usa.

Trazaré, pues, un cateto.

Yo no me meto, yo no me meto.

Triángulo, tetrágono, pentágono, hexágono, heptágono, octógono, son todos polígonos.

Seno, coseno, tangente y secante, y la cosecante y la cotangente.

Thales, Thales de Mileto

Thales, Thales de Mileto

Thales, Thales de Mileto

Thales, Thales de Mileto

Que es lo que queríamos demostrar.

¡Queesque loqueloque queriariamos demodemostrar!

2. Lugares geométricos

 2.1. ¿Qué es un lugar geométrico?

Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. La propiedad geométrica que define el lugar geométrico, tiene que traducirse al lenguaje algebraico de ecuaciones.

 2.2. La mediatriz y la bisectriz

• La mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan de los extremos.

• La bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de las rectas que forman el ángulo.

  2.3. Las cónicas

   2.3.1. ¿Qué son las cónicas?

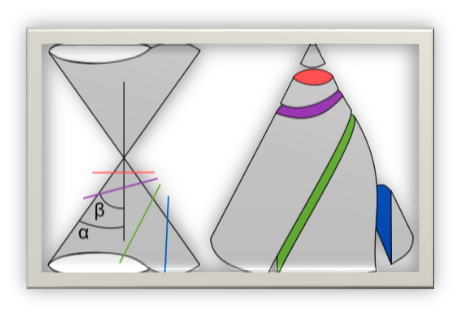
Las cónicas son curvas planas obtenidas mediante la intersección de un cono con un plano. El ángulo que forma el plano y el eje del cono comparado con el ángulo que forman el eje y la generatriz del cono determinan las distintas clases de cónicas.

   2.3.2. La circunferencia

La circunferencia es una linea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo.

Los elementos de la circunferencia son:

• Centro de la circunferencia: el centro es el punto del que equidistan todos los puntos de la circunferencia.
• Radio de la circunferencia: el radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
• Cuerda: la cuerda es un segmento que une 2 puntos de la circunferencia.
• Diámetro: es una cuerda que pasa por el centro de la circunferencia.
• Arco: un arco es cada una de las partes en que una cuerda divide a la circunferencia.
• Semicircunferencia: una semicircunferencia es cada uno de los puntos iguales que abarca el diámetro.

   2.3.3. La elipse

Es el lugar geométrico de los puntos del plano cuya suma de distancias a 2 puntos fijos llamados focos es constante.

Elementos de la elipse:

• Focos: son los puntos fijos F y F'.
• Eje focal: es la recta que pasa por los focos.
• Eje secundario: es la mediatriz del segmento FF'.
• Centro: es el punto de intersección de los ejes.
• Radios vectores: son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.
• Distancia focal: es el segmento de longitud 2C, C es el valor de la semidistancia focal.
• Vértices: son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
• Eje mayor: es el segmento de longitud 2A, A es el valor del semieje mayor.
• Eje menor: es el segmento de longitud 2B, B es el valor del semieje menor.
• Ejes de simetría: son las rectas que contienen al eje mayor o al eje menor.
• Centro de simetría: coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.

   · Obtención de un cono

   · El método del jardinero

Una elipse es una circunferencia achatada con dos ejes desiguales; el eje mayor, que mide 2a, lo situaremos en el eje X y el eje menor, que mide 2b, lo situaremos en el eje Y, de forma que el óvalo de la elipse quedará horizontal. 

Primero deben dibujarse perpendicularmente los dos ejes de coordenadas en el suelo y situar el eje Y en la dirección N-S, y el eje X en la dirección E-O. 

Luego hemos de señalar los dos focos que están en el eje X a ambos lados del centro a una distancia c, es decir, en los puntos (c,0) y (-c, 0). 

Después, con una cuerda que tenga de longitud l = 2a y colocando los extremos en los focos señalados, dibujar la elipse tal como se ve en la figura.

Esto es prácticamente todo. Sólo tendremos que señalar en la elipse los puntos horarios y los puntos que en el eje Y señalarán nuestra posición.

   · Mesa de billar elíptica

Coloca la bola en el foco “F” e impúlsala con el taco en la dirección que quieras. Siempre entra en el agujero, salvo imperfecciones en la nivelación o excesivo efecto en la bola. 

También entrará la bola si la lanzas desde otro sitio pero la haces pasar por el foco “F”. 

En una elipse, las líneas que unen los focos con un punto cualquiera de la curva forman con ella (con su tangente) ángulos iguales. Luego si la bola viene por una de esas líneas, después de “reflejarse” en la curva seguirá por la otra línea y, por tanto, pasará por el otro foco. Ahí hemos puesto el agujero.

   2.3.4. La hipérbola

Es el lugar geométrico de los puntos del plano cuya diferencia de distancias a 2 puntos fijos llamados focos es constante.

Elementos de la hipérbola:

• Focos: son los puntos F y F'
• Eje principal o real: es la recta que pasa por los focos.
• Eje secundario o imaginario: es la mediatriz del segmento FF'.
• Centro: es el punto de intersección de los ejes.
• Vértices. los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal. Los puntos B y B´ se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y. de radio, c.
• Radios vectores: son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'. 
• Distancia focal: es el segmento de longitud 2c.
• Eje mayor: es el segmento de longitud 2a.
• Eje menor: es el segmento de longitud 2b.
• Asíntotas: son las rectas de ecuaciones. y=- b/a·x, y=b/a·x.
• Relación entre semiejes: c^2= a^2 + b^2.

   · Lámpara hipérbolica

Son lámparas que al estar encendidas emanan un cono de luz hacia arriba y otro hacia abajo, los cuales forman sobre la pared 2 figuras con forma de hipérbole.

Las figuras sobre la pared, formadas por la luz de la lámpara, se pueden reproducir.

   2.3.5. La parábola

Hablando de las parábolas, me acabo de acordar de un chiste de parábolas, aquí lo dejo:

Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos:

y = ax² + bx + c

¿Y eso qué es? Dijo uno de los discípulos. 

A lo que Jesús respondió:  ¡Una parábola!

Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
Elementos de la parábola:

• Foco: es el punto fijo.

• Directriz: es la recta fija.

• Parámetro: es la distancia del foco a la directriz.

• Eje: es la recta perpendicular a una directriz que pasa por el foco.

• Vértice: es el punto de intersección de la parábola con su eje.

• Radio vector: es un segmento que une un punto cualquiera de la parábola con el foco.

3. Movimientos en el plano.

Chistes de... ¿matemáticas?

Sí, justo como habéis leído en el título, hoy os traigo unos cuantos chistes de matemáticas, atentos, porque, algunos, ¡son muy buenos!

• ¿Qué le dice la calculadora a un estudiante de matemáticas? Puedes contar conmigo.
• El 20 por ciento de las personas muere a causa del tabaco. Por lo tanto, el 80 por ciento de las personas muere por no fumar. Así que queda demostrado que no fumar es peor que fumar. (No fuméis, solo era un chiste).
• El 33 % de los accidentes mortales involucran a alguien que ha bebido. Por tanto, el 67 % restante ha sido causado por alguien que no había bebido. A la vista de esto, esta claro que la forma más segura de conducir es ir borracho y a toda pastilla. (Este sigue la temática del anterior, sigue siendo broma, no lo hagáis ¬¬'').
• ¿Qué es un oso polar. Un oso rectangular, después de un cambio de coordenadas. (Te lo dedico, Fernando, por lo del trabajo de funciones).
• ¿Quién invento las fracciones? Enrique Octavo.
• Me gustan los polinomios, pero solo hasta cierto grado.
• ¿Por qué se suicidó el libro de matemáticas? ¡Porque tenía muchos problemas!
• 2P2A + A2 y + K2 x 1/5 = KK (Léase en voz alta).
• Le pregunta un amigo a otro: ¿Sabes chistes de matemáticas? Y le responde el otro amigo: más o menos.

Bueno, estos son todos los chistes que subo hoy, pero, sin duda, ¡habrán más próximamente!

Excusas para no hacer los deberes de matemáticas

¿Cuántas veces no se nos ha olvidado hacer los deberes y no hemos tenido manera de librarnos? Ahora, os traigo la solución para ello.

A continuación, tenéis unas cuentas excusillas para no hacer los deberes de matemáticas.

• Es que tengo una calculadora solar, y como estaba nublado...
• Sé como comprobarlo, pero es que este margen es muy pequeño.
• Metí los deberes en la carpeta y la cerré pero vino un perro tetradimensional y se los comió.
• Juraría que los guardé en una botella de Klein, pero esta mañana no estaban.
• Estaba viendo el partido de fútbol cuando se me ocurrió comprobar si convergía... y claro, no e dio tiempo a hacer los deberes

Recomiendo que los uséis, pero con moderación, y solo una vez cada uno, porque, si no, al final os pillan, jejejejeje.

Cuestionario: funciones matemáticas

PRIMERA PARTE

Pregunta: ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo?

Respuesta: Mediante el uso de funciones.

Pregunta: ¿Qué es una función? ¿De qué formas pueden expresarse las relaciones entre magnitudes? Pon ejemplos de funciones de la vida cotidiana.

Respuesta: Una función es la relación entre dos magnitudes de manera que a cada valor de la primera le corresponde un único valor de la segunda. Se pueden expresar mediante fórmulas, tablas, etc. Mediante las proporciones. Por ejemplo, el crecimiento de un bebé, o las ganancias o pérdidas de una empresa.

Pregunta: ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y decrecientes? Puedes utilizar ejemplos gráficos para responder

Respuesta: Es el incremento de una función, que mide lo que cambia la función al pasar de un punto a otro. En las crecientes, toma un valor superior a 0 (positivo), y, en las decrecientes, toma un valor menor a 0 (negativo).

Pregunta: Utilizando la representación gráfica de una o varias funciones, explica las diferencias entre máximos y mínimos absolutos y relativos.

Respuesta: El máximo absoluto en una función, es cuando la ordenada es mayor o igual que en cualquier otro punto del dominio de la función. Por otro lado, la función tiene su mínimo absoluto si la ordenada es menor o igual a cualquier otro punto de la función.

Máximo y mínimo absoluto

La función tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a. En cambio, La función tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.

Máximo y mínimo relativo

Pregunta: Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría.

Función simétrica par

Función simétrica par: Si una función f verifica que f(x)=f(-x), se dice que la función es par y entonces su gráfica es simétrica respecto del eje OY.

Función simétrica impar

Función simétrica impar: Si una función verifica que f(-x)=-f(x), se dice que es función impar y entonces su gráfica es simétrica respecto del origen de coordenadas O(0,0).

Pregunta: Representa gráficamente una función periódica indicando por qué se denomina de esa forma.

Respuesta: Las funciones periódicas son aquellas en las que tienen ondas que muestran periodicidad respecto al tiempo, es decir, describen ciclos repetitivos.

Función periódica coseno

Pregunta: Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia entre ambas?

Función continua: Una función es continua cuando su gráfica es una linea seguida, no interrumpida

Función continua (izquierda) y función discontinua (derecha)

Función discontinua: Una función es discontinua cuando su función f es definida en un intervalo abierto y es interrumpida.
Pregunta: Investiga: ¿Cuál es el origen del término función?

Respuesta: Nació ligado a la idea de dependencia de cantidades variables, en unión al estudio del movimiento, en época de Galileo Galilei, y con la caracterización dada por Nicolás de Oresme: "Todo lo que varía, se sepa medir o no, lo podemos imaginar como una cantidad continua representada por un segmento". Esta concepción de carácter físico y geométrico antecedió a la noción cartesiana de dependencia numérica.
Este concepto resultó demasiado restrictivo para las necesidades de la física matemática, por lo que la idea de función debió pasar por un largo proceso de generalización y clarificación.

SEGUNDA PARTE

Pregunta: Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora una tabla resumen con todas las gráficas obtenidas.

 a) Función lineal creciente: Click aquí

 b) Función lineal constante: Click aquí

 c) Función lineal decreciente: Click aquí

 d) Rectas paralelas: Click aquí

 e) Función cuadrática cóncava: Click aquí

 f) Función cuadrática convexa: Click aquí

Pregunta: Investiga sobre la representación de funciones en coordenadas polares.

Respuesta: Las coordenadas polares o sistemas polares son un sistema de coordenadas dimensional en el cual cada punto del plano se determina por una distancia y un ángulo, ampliamente utilizados en física y trigonometría.

Pregunta: Utilizando uno de los programas anteriores investiga sobre la representación gráfica de

funciones en el espacio (x, y, z).

 a) z = x

 b) 2

 c) + y

Pregunta: Utiliza el programa que has elegido para resolver gráficamente el sistema de dos ecuaciones lineales con dos incógnitas siguiente:

 a) 2 3 33

 b) 3 2 4

 c) x y

Pregunta: Elige un modelo de coche que disponga de motorizaciones diesel y gasolina y realiza un estudio gráfico de la función coste que nos permita averiguar cual es el automóvil más adecuado para nosotros en función del número de kilómetros que recorremos anualmente. (Nota: Necesitas el precio del coche, el del combustible y el consumo combinado)

Pregunta: Interpreta la gráfica del recorrido del Maratón Popular de Madrid

Pregunta: Explora el uso del programa SURFER en imaginary

Refuerza y amplía tus matemáticas

Hola chic@s, aquí os dejo algunos canales que, generalmente, uso para resolver dudas y repasar mis matemáticas. 

Además, la mayoría responden a los comentarios en sus vídeos si no habéis entendido algo.

• Unicoos: clic aquí
• Julioprofe: clic aquí
• Cibermatex: clic aquí

También uso algunas páginas web, que te diré a continuación:

• Vitutor: clic aquí
• Va de números: clic aquí
• Las matemáticas: clic aquí